Логические парадоксы

🧩 Что такое апории? В древнегреческой философии начиная с 5 века до нашей эры начинают приобретать особый вес апории — «безвыходные рассуждения». Для греков состояние апории было не симптомом провала или логической катастрофы, а констатацией того, что мысль зашла в тупик и нужно «скорректировать маршрут». Такие парадоксы чаще всего были связаны с категориями бытия — движением и покоем, единством и множественностью. Размышления над ними привели к развитию широкого спектра философских систем — от платоновского объективного идеализма до демокритовского атомистического материализма.

Рассмотрим апорию «Ахиллес и черепаха»👇

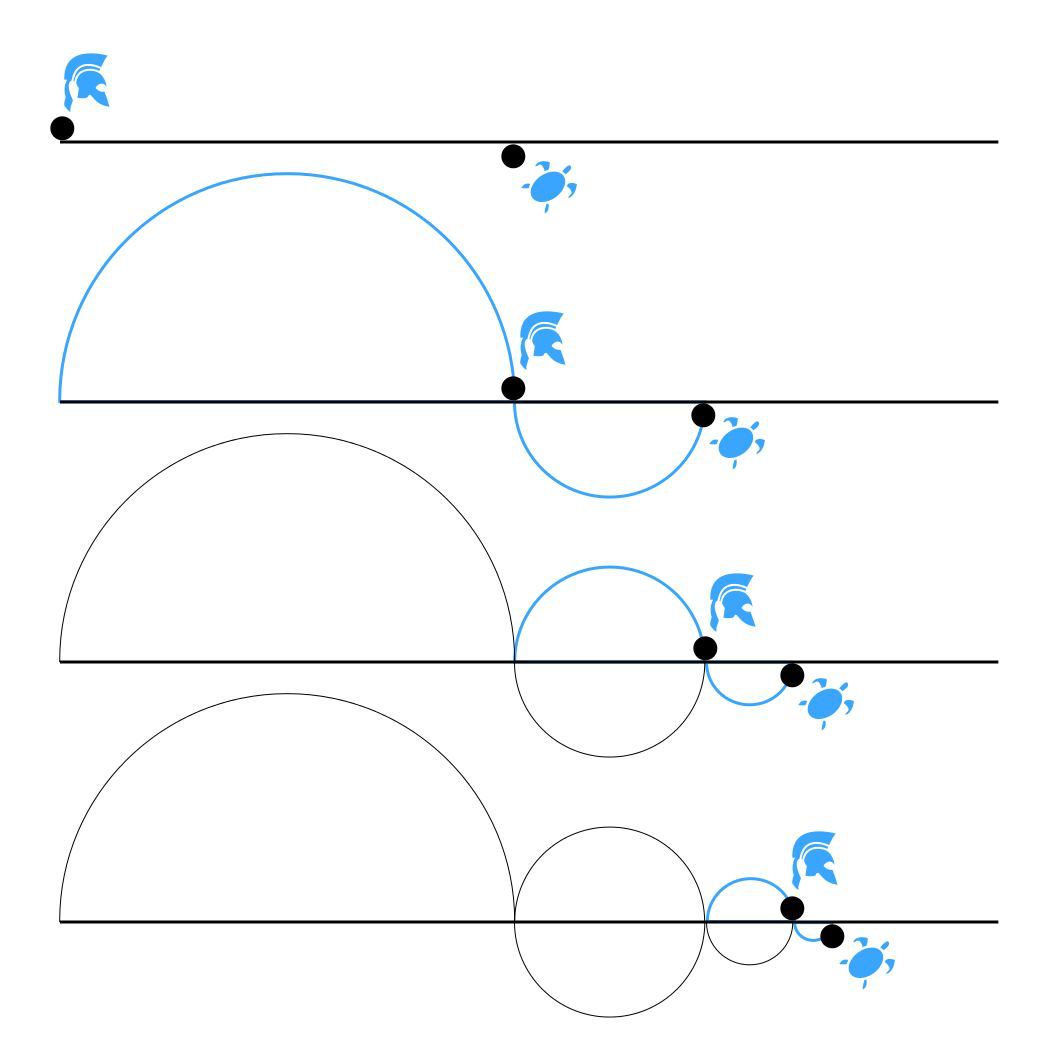
🐢 «Ахиллес и черепаха» — самая известная апория, принадлежащая Зенону Элейскому (5 век до нашей эры). Впрочем, иногда ее авторство приписывается учителю Зенона — Пармениду. В ней Зенон, развивая парменидовскую критику понятия движения, доказывает, что мы неспособны помыслить относительное движение двух тел — например, как одно тело догоняет другое.

🏃‍♂️ Представим ситуацию: быстроногий Ахиллес и медлительная черепаха состязаются в беге. Ахиллес стартует позади черепахи и вынужден ее догонять. Догонит ли он черепаху?

💡 Будем рассуждать логически. Для того чтобы догнать кого-то, надо сначала оказаться в той точке, где он сейчас находится. Перемещаясь в эту точку, Ахиллес потратит определенное время (его скорость велика, но не бесконечна). За это время черепаха хотя и медленно, но все же уползет на некоторое расстояние вперед.

🔄 Ситуация повторяется: чтобы догнать черепаху, Ахиллес должен сначала переместиться туда, где она находится в данный момент, и затраченное на это время даст черепахе возможность уползти еще немного вперед.

➡️ По мнению Зенона, мы вынуждены повторять это умозаключение бесконечно и каждый раз будем приходить к одному и тому же выводу: расстояние между Ахиллесом и черепахой сокращается, но никогда не будет равно нулю.

⁉️ Этот вывод противоречит как здравому смыслу, так и нашему опыту. Но Зенон пытался привлечь внимание современников к тому обстоятельству, что опыт и здравый смысл не всегда лучшие помощники в поисках истины. С точки зрения разума, считал он, движения не существует, ведь его невозможно помыслить. При этом Зенон не отрицал, что оно существует для наших чувств. Философы должны сами решить, чему доверять — чувствам или разуму.

Ахиллес и черепаха

В апории «Дихотомия» Зенон доказывает невозможность движения даже одного тела — а именно, невозможность переместиться из точки А в точку Б за любое конечное время.

➗ Дихотомия — деление пополам. Такое название этому рассуждению, судя по источникам, дал Аристотель.

⏱ Представим, что путник отправляется из точки А в точку Б и движется с некой конечной скоростью. Сможет ли он пройти этот путь за конечное время?

💡 Будем рассуждать логически. Чтобы пройти весь путь, сначала надо пройти его половину. А чтобы пройти половину, необходимо сначала пройти половину половины, то есть четверть. А чтобы пройти четверть… В общем, вы уже поняли, что этот ход мысли можно повторять бесконечно.

➡️ Поскольку пространство континуально, у любого, даже самого малого отрезка найдется своя середина. Значит, любой конечный отрезок можно разбить на бесконечное количество «половинок». Но бесконечное количество отрезков за конечное время преодолеть невозможно, считал Зенон.

⁉️ Противоречие: мы не можем помыслить, как движущееся тело преодолевает конечное расстояние за конечное время, хотя на практике наблюдаем это постоянно.

Апория «Стрела» показывает, что мы не можем помыслить не только результат движения — как движущееся тело догоняет другое или преодолевает какое-то расстояние, — мы не можем помыслить даже сам процесс движения.

🏹 Зенон предлагает нам представить летящую стрелу. А затем спрашивает: как именно стрела летит? Обладает ли стрела определенными размерами? Безусловно. Сохраняются ли эти размеры, пока стрела летит? Разумеется. Не означает ли сказанное, что в любой момент времени стрела занимает строго определенное место, ограниченное ее размерами? Конечно же, означает.

🔜 Откуда берется движение? Если в любой момент времени стрела занимает в пространстве строго определенное место, значит, в каждый момент она покоится.

⁉️ Противоречие: движение не может получаться из суммы статических состояний, и в то же время, наши чувства и опыт свидетельствуют, что в окружающем мире движение постоянно происходит.

Стрела Зенона

Как философы отреагировали на эти и другие зеноновские апории движения? Очень по-разному, и это замечательно, потому что поиск решения неразрешимых, казалось бы, проблем, толкал философию и науку вперед.

Рассмотрим некоторые варианты решения апорий👇

⚛️ Решение атомистов. Левкипп, Демокрит и другие древнегреческие философы-атомисты пришли к выводу, что корень парадоксов движения — аксиома бесконечной делимости пространства и времени. Достаточно признать, что существуют некие неделимые величины, как бесконечный регресс зеноновских рассуждений прекращается. Попросту говоря, когда между Ахиллесом и черепахой остается неделимый квант пространства, он преодолевает его одномоментно, за 0 секунд, и так догоняет черепаху.

📐 Решение Аристотеля. Аристотель больше всех других античных философов рассуждал над поставленными Зеноном проблемами. Он обнаружил, что их корень лежит в смешении двух видов бесконечности — потенциальной и актуальной. Примером потенциальной бесконечности может служить натуральный ряд чисел — он все время продолжается вправо, так как за каждым числом следует еще большее. Но в то же время, неверно было бы утверждать, что существует актуально бесконечное число (число, которое больше всех остальных чисел). В рассуждениях Зенона предполагается, что мы мысленно уже поделили отрезки на бесконечное количество частей, что на самом деле невозможно — можно лишь делить их все дальше и дальше.

🔢 Решение науки Нового времени. В Новое время ученые (Ньютон и Лейбниц), наконец, разработали математический аппарат, с помощью которого оказалось возможным строго помыслить движение, не впадая при этом в противоречия. Был создан математический анализ — дифференциальное исчисление позволяло раскладывать континуальные величины на бесконечно малые, но ненулевые слагаемые, а интегральное исчисление позволяло складывать из них обратно тот континуум, который был подвергнут делению.

Готфрид Вильгельм Лейбниц и Исаак Ньютон

Диодор Кронос и парадокс невозможности движения